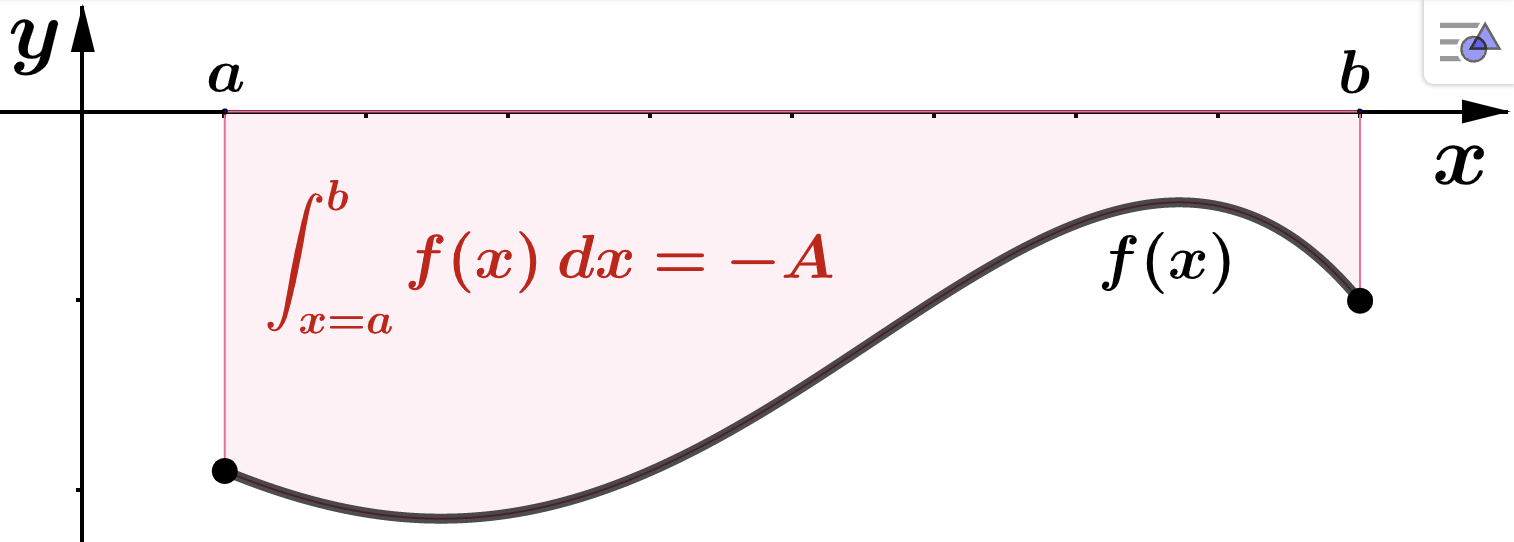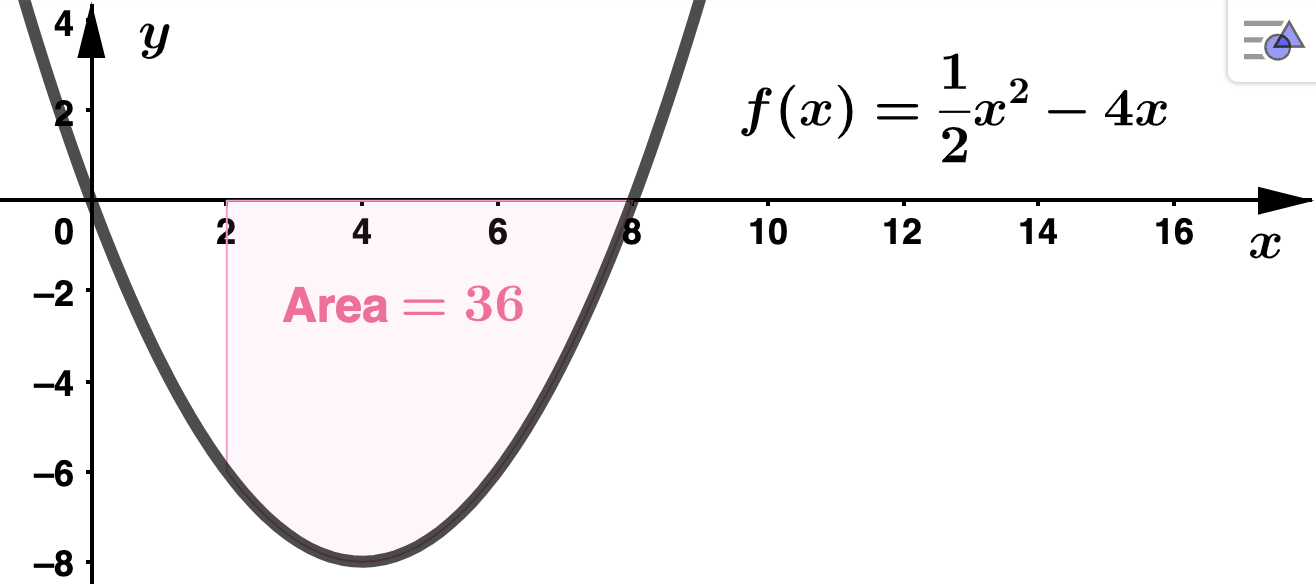Skip to main content

Business Mathematics: Applications Using Algebra and Calculus

Alfred Dahma

Section 4.3 The Fundamental Theorem of Calculus

Remark 4.3.2.

  • The vertical bar to the right of \(F(x)\) in the FTC is called an evaluation bar. By definition,
    \begin{equation*} F(x) \Big|_{x=a}^{b} = F(b) - F(a) \end{equation*}
  • The statement "let \(F(x)\) be any anitderivative of \(f(x)\)" in the FTC means that we can choose any antiderivative \(F\) of \(f\) we want. Recall that antiderivatives can only be determined up to an arbitrary constant \(c\text{.}\) So, we can CHOOSE the constant for our antiderivative when evaluating a definite integral. Unless indicated otherwise, we will always choose \(c=0\text{.}\) Note that this means there is no "\(+ c\)" when you calculate a definite integral. Definite integrals will produce an exact value.
Geometric Interpretation of Definite Integrals
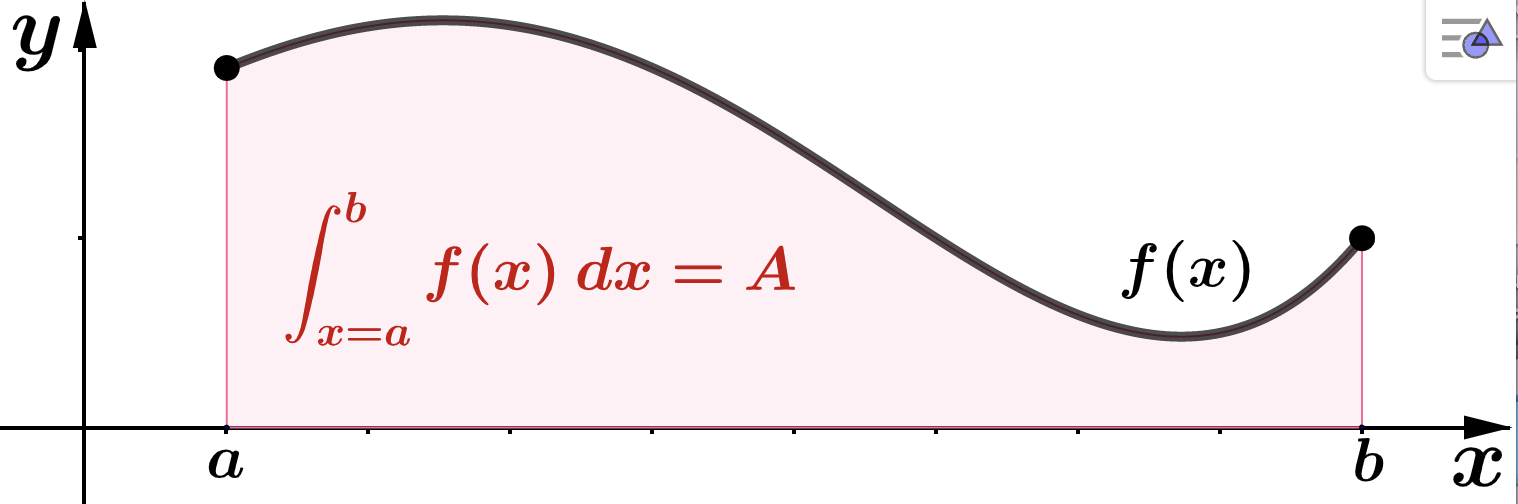
In each item below, \(A\) represents the area between the graph of \(f\) and the interval \([a,b]\text{.}\) Notat that area \(A\) is always greater than or equal to 0: \(A \geq 0\text{.}\)
  • Suppose \(f(x) \geq 0\) and \(F'(x)= f(x)\) (\(f\) is the rate of change of \(F\)) for every \(x\) in the interval \([a,b]\text{.}\) Then
    \begin{equation*} \int_{x=a}^{b} f(x) \: dx = A = F(b) - F(a) \geq 0 \end{equation*}
    Note that this is just a restatement of Fact 4.2.1
  • Suppose \(f(x) \leq 0\) and \(F'(x)= f(x)\) (\(f\) is the rate of change of \(F\)) for every \(x\) in the interval \([a,b]\text{.}\) Then
    \begin{equation*} \int_{x=a}^{b} f(x) \: dx = - A = F(b) - F(a) \leq 0 \end{equation*}
Properties of the Definite Integral
Assume that \(f\) and \(g\) are integrable on \([a,b]\) and let \(c\) and \(k\) be real numbers.
  1. \(\displaystyle \int_{x=a}^{b} k f(x) \: dx = k \int_{x=a}^{b} f(x) \: dx\)
  2. \(\displaystyle \int_{x=a}^{b} (f(x) \pm g(x)) \: dx = \int_{x=a}^{b} f(x) \: dx \pm \int_{x=a}^{b} g(x) \: dx\)
  3. \(\displaystyle \int_{x=a}^{b} f(x) \: dx = \int_{x=a}^{c} f(x) \: dx + \int_{x=c}^{b} f(x) \: dx \)
  4. \(\displaystyle \int_{x=a}^{b} f(x) \: dx = - \int_{x=b}^{a} f(x) \: dx \)
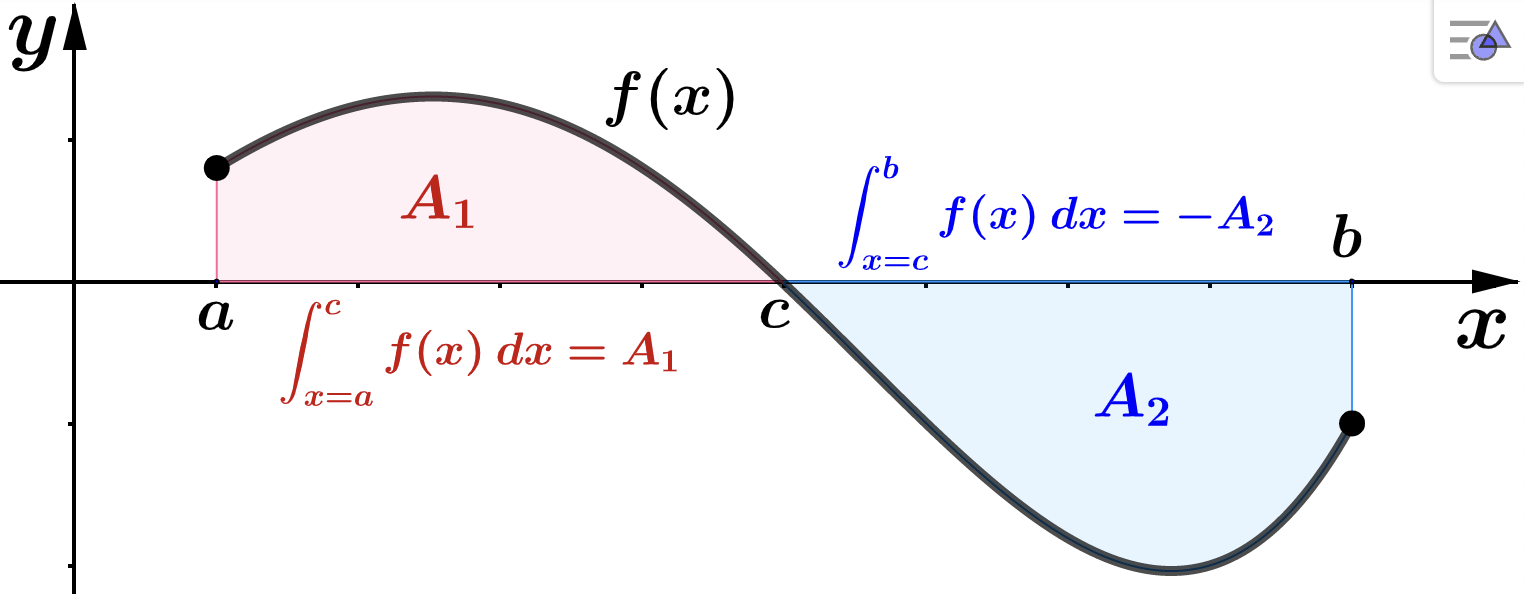
Property (3) in the above list gives us a way to geometrically interpret a definite integral in case \(f(x)\) crosses the horizontal axis in between \(x=a\) and \(x=b\text{,}\) at say \(x=c\text{.}\) Suppose \(f(c) = 0\text{,}\) \(f(x) \geq 0 \) on \([a,c)\text{,}\) and \(f(x) \leq 0\) on \((c,b]\text{.}\) Let \(A_1\) be the area between the graph of \(f(x)\) and the interval \([a,c)\) and let \(A_2\) be the area between the graph of \(f(x)\) and the interval \((b,c]\text{.}\) Then
\begin{align*} \int_{x=a}^{b} f(x) \: dx \amp = \int_{x=a}^{c} f(x) \: dx + \int_{x=c}^{b} f(x) \: dx \\ \\ \amp = \qquad A_1 \qquad + \qquad (-A_2)\\ \\ \amp = \qquad A_1 \qquad - \qquad A_2 \end{align*}
Let's summarize the interpretations of the defnite integral:
Suppose \(f\) is integrable on \([a,b]\) and \(F' = f\text{.}\) On the interval \([a,b]\text{,}\) let \(A_1 = \) area above the \(x\)-axis and under the graph of \(f\) and let \(A_2 = \) area below the \(x\)-axis and above the graph of \(f\) (note that \(A_1\text{,}\) \(A_2 \geq 0\) since they represent area).
  • Geometric Interpretation
    \begin{equation*} \int_{x=a}^{b} f(x) \: dx = A_1 - A_2 \end{equation*}
  • Physical Interpretation
    \begin{equation*} \int_{x=a}^{b} f(x) \: dx = F(b) - F(a) = \: \textrm{total change in} \: F \: \textrm{from} \: x= a \: \textrm{to} \: x=b \end{equation*}
Evaluate the following definite integrals using either the area interpretation of the definite integral or Theorem 4.3.1.
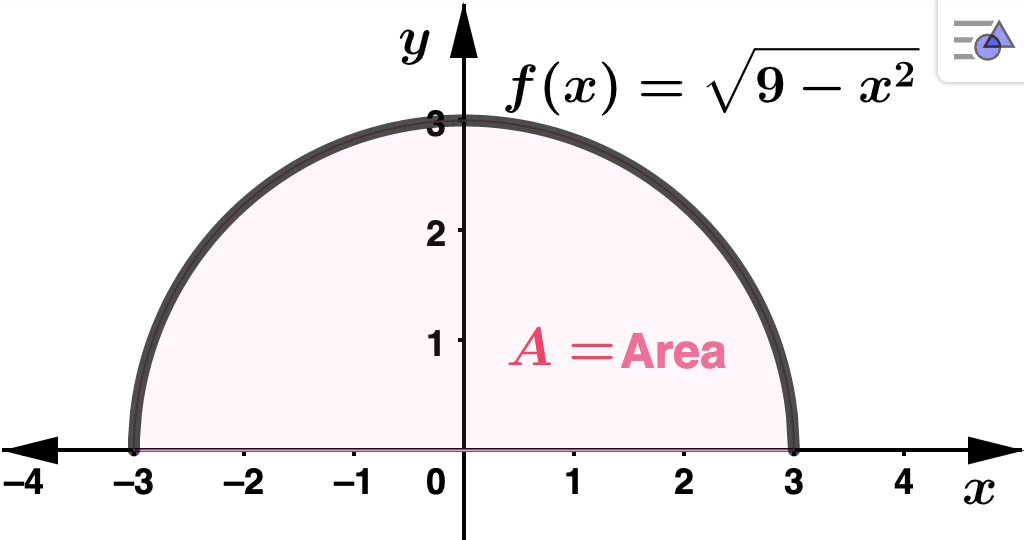
  1. \(\displaystyle \int_{x=-3}^{3} \: \sqrt{9-x^2} \: dx\) Solution.
    We will NOT be able to use the Theorem 4.3.1 for this problem because we will not be able to find an antiderivative for \(f(x) = \sqrt{9-x^2}\text{.}\) However \(f(x)\) is the upper half of the circle centered at the origin with radius \(r=3\text{,}\) so we CAN use the geometric interpretation of the definite integral as area. Recall that the formula for the area of a circle with radius \(r\) is \(\pi \cdot r^2\text{.}\)
    Letting \(A\) represent the area of the shaded region above,
    \begin{equation*} \int_{x=-3}^{3} \: \sqrt{9-x^2} \: dx = A = \dfrac{\pi}{2} \cdot 3^2 = \dfrac{9 \pi}{2} \end{equation*}
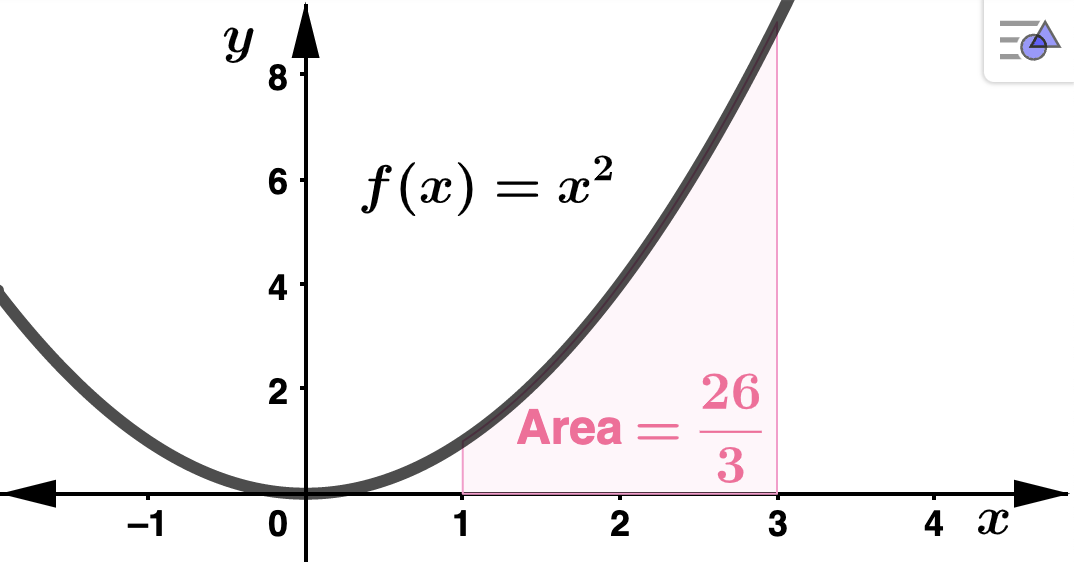
  2. \(\displaystyle \int_{x=1}^{3} x^2 \: dx \) Solution.
    Here we use Theorem 4.3.1. Notice the choice of \(c=0\) in the antiderivative.
    \begin{equation*} \int_{x=1}^{3} x^2 \: dx = \left(\dfrac{1}{3}x^3\right) \Biggr|_{x=1}^{3} = \dfrac{1}{3} (3^3 - 1^3) = \dfrac{26}{3} \end{equation*}
  3. \(\displaystyle \int_{x=2}^{8} \left(\dfrac{1}{2}x^2 - 4x \right) \: dx \) Solution.
    Again we can use Theorem 4.3.1, choosing \(c=0\) for the integration constant.
    \begin{align*} \int_{x=2}^{8} \left(\dfrac{1}{2}x^2 - 4x \right) \: dx \amp = \left(\dfrac{1}{6}x^3 - 2x^2\right) \Biggr|_{x=2}^{8}\\ \\ \amp = \left(\dfrac{1}{6} \cdot 8^3 - 2\cdot 8^2 \right) - \left(\dfrac{1}{6} \cdot 2^3 - 2\cdot 2^2 \right) \\ \\ \amp = -36 \end{align*}
    Notice that \(\dfrac{1}{2}x^2 - 4x \leq 0\) on the interval \([2,8]\text{,}\) so the value of the definite integral and the area (which is always postive) have opposite signs.
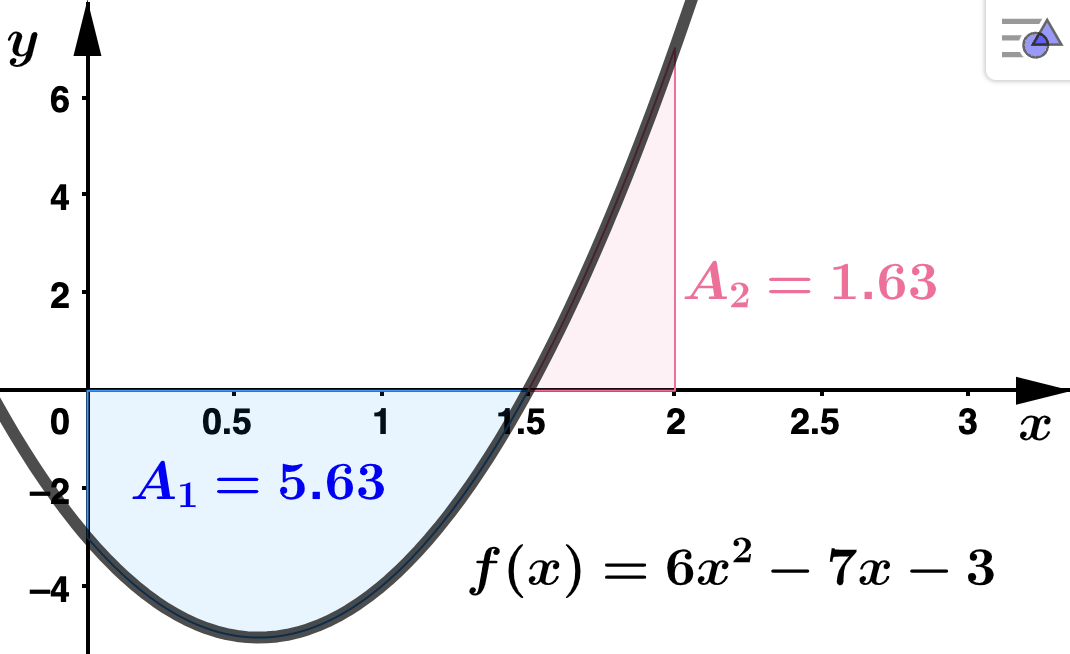
  4. \(\displaystyle \int_{x=0}^{2} (6x^2 - 7x -3) \: dx \) Solution.
    Using Theorem 4.3.1 with \(c=0\)
    \begin{equation*} \int_{x=0}^{2} (6x^2 - 7x -3) \: dx = = (2 \cdot 8^3 - \dfrac{7}{2} \cdot 8^2 - 3 \cdot 8) - (0) = -4 \end{equation*}
    Observe that \(6x^2 - 7x -3\) crosses the \(x\)-axis at \(x = 1.5\text{,}\) where it changes from negative to positive. Using property 3 above and the area labels in the graph
    \begin{align*} \int_{x=0}^{2} (6x^2 - 7x -3) \: dx \amp = \int_{x=0}^{1.5} (6x^2 - 7x -3) \: dx + \int_{x=1.5}^{2} (6x^2 - 7x -3) \: dx \\ \\ \amp = -A_1 + A_2 \\ \\ \amp = -5.63 + 1.63\\ \\ \amp = -4 \end{align*}
<Prev^TopNext>
Authored in PreTeXt
Powered by Runestone