Section 2.5 General Polynomials
Definition 2.5.1.
A polynomial is a function that can written in the form
\begin{equation*}
p(x) = a_nx^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} +\cdots +a_2x^2 + a_1x + a_0
\end{equation*}
where \(n\) is a whole number and \(a_n, a_{n-1}, \ldots , a_1, a_0\) are real numbers called coefficients. If \(a_n \neq 0\) then \(n\) is called the degree of the polynomial, which is expressed by writing deg(\(p\)) = \(n\text{.}\) In this case the number \(a_n\) is called the leading coefficient, and \(a_nx^n\) is called the leading term.
Some examples of polynomials:
\(\displaystyle p(x) = 2x^4 -7.5x^3 - \frac{1}{2}x-12 \)
\(\displaystyle g(t) = 2 - t^7 \)
\(\displaystyle q(p) = -3 \)
For homework, identify the degree, leading term, and leading coefficient of each of the polynomials above.
Some examples of functions that are NOT polynomials:
\(\displaystyle f(x) = \dfrac{2}{x}+4 \)
\(\displaystyle h(t) = t^3 + \sqrt{t} \)
\(\displaystyle r(p)= 3^p - p \)
For homework, use
Definition 2.5.1 to explain why the above functions are not polynomials.
For the polynomial \(p(x)\text{,}\) as \(x\) approaches \(\infty\) or \(-\infty\text{,}\) \(p(x)\) becomes forever increasing or decreasing. This is referred to as the "end behavior" of the polynomial and is entirely determined by the leading term, \(a_nx^n\text{.}\)
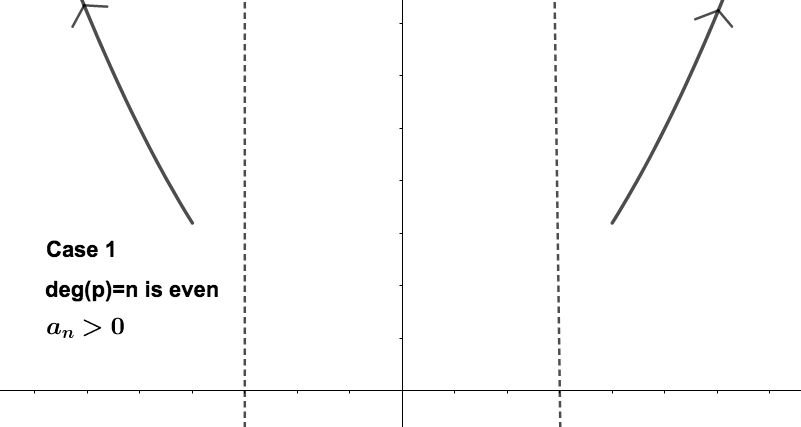
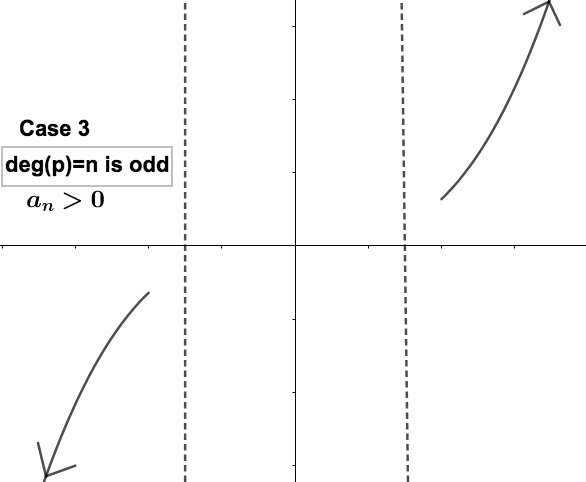
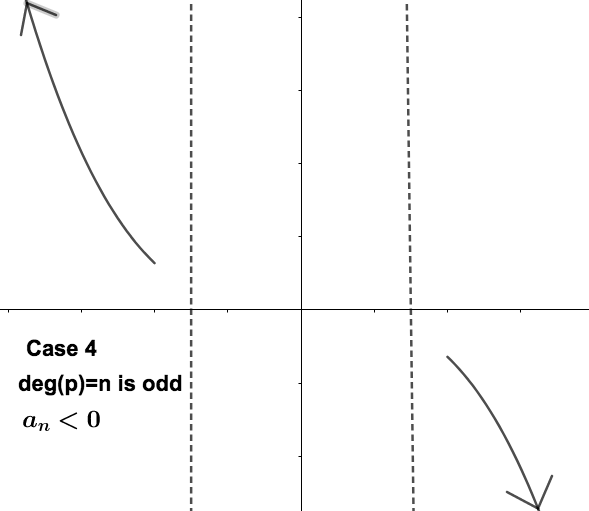
The Leading Term Test tells us that there are 4 possibilities for the end behavior of polynomials, pictured below. The gap inside the dotted lines indicates we cannot predict the behavior of the polynomial near the origin. This test explains what happens to the polynomial at the far ends of the horizontal axis. The behavior depends on the degree of the polynomial being odd or even, and the sign of the leading coefficient.
Cases 1 and 2: End behavior of even degree polynomials, such as
\(x^2\) and
\(-x^2\)
Cases 3 and 4: End behavior of odd degree polynomials, such as
\(x^3\) and
\(-x^3\)
Example 2.5.2.
Identify the end behavior of the polynomial \(p(x) = \dfrac{6}{7}(x-9)^4(x+4)^2(5-3x)\) Solution.First you should convince yourself that this is indeed a polynomial. We just need to identify the leading term, which will be the product of the leading terms of each factor:
\begin{equation*}
\dfrac{6}{7}(x^4)(x^2)(-3x) = -\dfrac{18}{7}x^7
\end{equation*}
So, the end behavior is as in Case 4 above.
Let \(p(x)\) be a polynomial, deg(\(p\)) = \(n\text{.}\) Then
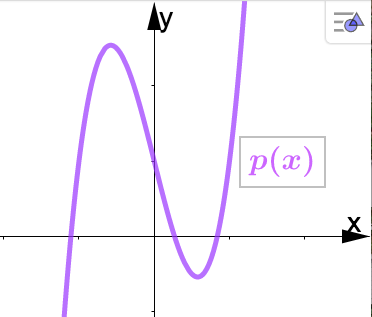
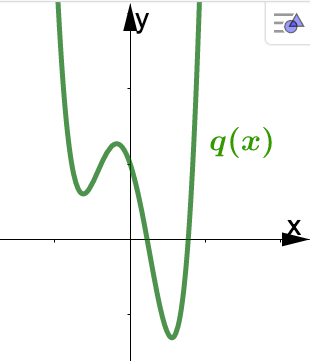
Let Identify the smallest possible degree of the polynomials in the graphs below.
In the graph on the left (for \(p\)), the Leading Term Test tells us that deg(\(p\)) must be odd. Now, \(p\) has 2 turning points and 3 horizontal intercepts, which means deg(\(p\)) \(\geq 3\text{.}\)
In the graph on the right (for \(q\)), the Leading Term Test tells us that deg(\(q\)) must be even. Now, \(q\) has 3 turning points and 2 horizontal intercepts, which means deg(\(q\)) \(\geq 4\text{.}\)
Example 2.5.3.
The revenue and cost functions for ADTF Distributors are given by
\begin{align*}
R(t) \amp = -234t^3 +8139t^2-90,692t+388,407 \qquad \textrm{and} \\
C(t) \amp = -73t^3 + 2461t^2-26,151t+107,839
\end{align*}
in tens of millions of dollars where \(t\) is the number of years since 2012. Find ADTF Distributors' profit in 2021.